Estrazione veloce della radice
Cerca di svolgere il seguente compito a mente:
Quadratwurzel aus 75076 = ?
Risolvere una radice è un'operazione complessa. Questo lo possono fare solo pochi eletti senza l'uso della calcolatrice. I campioni del calcolo mentale la risolvono addirittura a mente.
Quando qualcuno parla di radice, si tratta in genere di radice quadrata. Cioè la seconda radice viene chiamata radice quadrata. Una radice è una potenza al contrario. Quando prendiamo la seconda potenza di 9 prendiamo 9 alla seconda oppure 9 x 9 = 81. Quando poi facciamo la radice di 81 il risultato è di nuovo 9. Questa è la seconda potenza o la radice quadrata. Come esempio qui le potenze da 1 a 32.

Quando vedi i risultati puoi stabilire che la potenza di 1 e 9 finisce sempre con 1. La potenza di 2 & 8 sempre con 4, la potenza di 3 & 7 sempre con 9 e la potenza di 4 & 6 si conclude sempre con 6. La potenza di 5 su 5 e quella di 0 su 0. Ciò è importante per il seguito.
A scuola abbiamo imparato così a fare la radice quadrata:
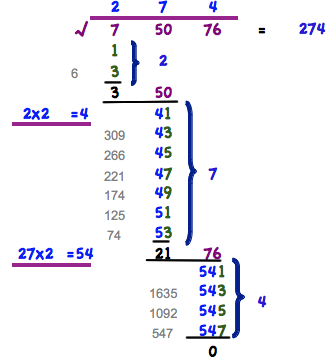
- 1. Numero a sinistra dividerlo in due gruppi
- 2. Adesso dal gruppo di sinistra tirare i numeri dispari. Cominciare con 1, finchè si ottiene un resto positivo! Cioè 7-1=6, 6-3=3, 3-5= -2 non va più.
- 3. Contare i numeri dispari. Se c'è 1. Cifra della soluzione (2).
- 4. Con il resto (3) inserire il secondo gruppo (50). Il risultato è 350.
- 5. Il risultato precedente moltiplicarlo per 2 (2x2=4). Questa è la nuova base alla quale alleghiamo i numeri dispari (4x) e tiriamo il valore (350).
- 6. Continuare come descritto al punto 2. 350-41=309; 309-43=266, 266-45...
- 7. Andare avanti come descritto in 3-5. 3. Cifra numero dispari (7), 2. Cifra della soluzione 4. Aggiungere successivo 2° gruppo (2176), 5. Risultato moltiplicarlo per 2 (27x2=54)
- 8. Continuare come descritto al punto 4. Resto (21) e successivo secondo blocco (76), risultato (2176). 2176-541=1635, 1635-543=1092,...
Un altro modo per risolvere una cifra al quadrato:
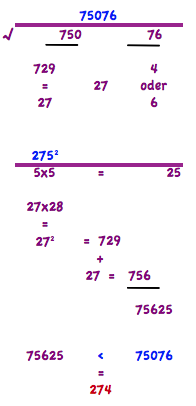
Facciamo un altro esempio per rendere chiara la spiegazione. Cerchiamo la radice di 12769. Questo diviso in due blocchi da 127 & 69. Termina con 9. Possibili potenze con 3 oppure 9. La potenza maggiore per la quale 127 non è divisibile è 11. Allora i possibili candidati sono 113 & 119. Adesso la potenza di 115. 11x11=121+11=132. 132 & 25= 13225. Il risultato è di nuovo 12769, quindi la radice di 12769= 113.
Così si memorizza tutto:
Poichè non ho trovato alcuna istruzione per l'uso degna di nota per l'utilizzo di una radice quadrata, attendo l'istruzione per l'uso di un calcolatore a mente.
Istruzioni per l'uso: Risolvi radice - Calcola radice quadrata
Hier geht es darum die Quadratwurzel aus einer fünfstelligen Zahl, im Kopf, zu ziehen. Mit etwas Übung wirst du das sicher schaffen.
Più bravo sei, più alto è il tuo livello.
Questa è la suddivisione dei livelli:
| Level | <=5 min | Aggiunta | × 5 Stellen | Aggiunta | × 8 Stellen | Aggiunta | <=5 min | Aggiunta |
|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| 2 | 2 | 0 | 2 | 0 | 2 | 0 | 2 | 0 |
| 3 | 3 | 0 | 3 | 0 | 3 | 0 | 3 | 0 |
| 4 | 4 | 0 | 6 | 0 | 4 | 0 | 4 | 0 |
| 5 | 5 | 0 | 9 | 0 | 5 | 0 | 5 | 0 |
| 6 | 6 | 0 | 12 | 0 | 6 | 0 | 6 | 0 |
| 7 | 6 | 1 | 12 | 3 | 6 | 1 | 6 | 1 |
| 8 | 7 | 1 | 15 | 3 | 7 | 1 | 7 | 1 |
| 9 | 8 | 1 | 18 | 3 | 8 | 1 | 8 | 2 |
| 10 | 9 | 1 | 21 | 3 | 9 | 1 | 10 | 2 |
| 11 | 10 | 1 | 24 | 3 | 10 | 1 | 12 | 2 |
| 12 | 11 | 1 | 27 | 3 | 11 | 1 | 14 | 2 |
| 13 | 12 | 1 | 30 | 3 | 12 | 1 | 16 | 2 |
| 14 | 12 | 2 | 30 | 6 | 12 | 2 | 16 | 4 |
| 15 | 13 | 2 | 33 | 6 | 13 | 2 | 18 | 4 |
| 16 | 14 | 2 | 36 | 6 | 14 | 2 | 20 | 4 |
| 17 | 15 | 2 | 39 | 6 | 15 | 2 | 22 | 4 |
| 18 | 16 | 2 | 42 | 6 | 16 | 2 | 24 | 4 |
| 19 | 17 | 2 | 45 | 6 | 17 | 2 | 26 | 4 |
| 20 | 20 | 0 | 54 | 0 | 20 | 0 | 32 | 0 |
 Menü
Menü
