
Um diesen Inhalt anzuzeigen muss eine Verbindung zu Youtube / Google hergestellt werden. Dabei werden von Ihrem Browser eventuell persönliche Daten übertragen und ausgewertet. Wollen Sie dennoch fortfahren?
Fast addition
Try to solve the following task by mental calculation:
484168 + 363143 + 123832 + 532557 + 176154 = ?
Addition is one of the four basic arithmetic operations. This discipline is most often used in everyday life. This discipline is considered relatively simple but it is a challenge nevertheless. If you should add something in written form, the best way is to put each number below each other. So you are faster and you can avoid oversights caused by searching. You've already noticed it in the example above.
In school we learned to do addition in the following way:
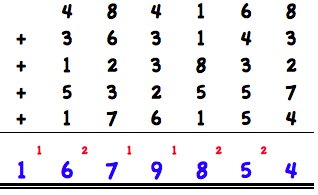
We start from the right and add the digits 8+3+2+7+4 = 24. The 4 has to be written under the dash and the 2 will be transferred to the next column. Then we take the 2nd column and add again 6+4+3+5+5+2 (the carry-over from column 1) = 25. We write the 5 under the dash and the 2 will be transferred to the next column. Now we take the 3rd column and add 1+1+8+5+4+1 (the carry-over from column 2) = 18. The 8 is written under the dash and the 1 will be transferred to the next column. I think the procedure should be clear. But you have survived the second class of elementary school.
Another method to add faster is to find couples of ten:
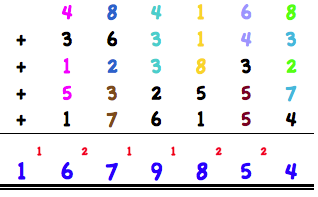
Here you need some practice not to lose track. We are always looking for ten couples, namely 9 & 1, 2 & 8, 7 & 3, 6 & 4, 5 & 5, etc.. We are starting with the right column to find a possible counterpart to the 8. The 2 is an appropriate counterpart. Then we look for a possible counterpart for 3. This is 7. 4 is the only number left. We found 2 pairs, namely 20 and 4. We write the numbers under the dash and transfer the number 2. Then we go to the next column. Here we find two pairs, namely 6 & 4 and 5 & 5. Number 3 & 2 (you have just carried over) is left. We write down 5 under the dash, 2 will be transferred. In the 3 column we find a pair of ten which consists of 3 digits, namely 1 & 1 & 8. Numbers 5, 1 and 2 are left. Then we write down 8 under the dash and transfer the number 1. I think that the procedure should be comprehensible.
Another method to add faster is to split digits in groups of 2:
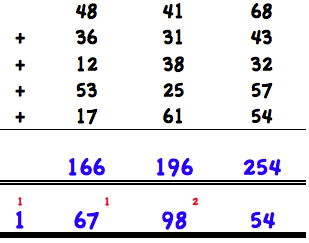
We split in groups of 2 digits. So we add 2 columns at once. 68 +43 +32 +57 +54 = 254. The next column is 41 +31 +38 +25 +61 = 196. The next column is 48 +36 +12 +53 +17 = 166. Now we have the 3 partial results of od the columns. Now we split again the partial results into groups of 2. That means we transfer the hundreds of one column to the left and add this together. We take 54 of 254 and write 54 under the dash. Then we add 2 to 196. Then we write 98 under the dash and transfer 1 and add it to 166. The last step is to write down 167 under the dash. If you feel comfortable dealing with large numbers, this method could be appropriate for you. It is a bit more difficult to find pairs of hundreds, but it is possible.
What is the best way to add quickly and easily?
There is no clear answer to this question. It depends on the method you feel most comfortable with. To find this method, you have to practice. The Spanish maths genius and Guinness record holder Alberto Cotto can add one hundred one-digit numbers within 17.04 seconds. This is an outstanding achievement and a Guinness record. He does not split figures into pairs of 10 but he adds the figures "just like that". Given that he can do it quicker than anyone, this is certainly the best method for him.
Instructions: Addition
Hier geht es darum so schnell wie möglich 10 zehnstellige Zahlen im Kopf zu addieren. Das möglichst schnell und Fehlerfrei. Mit etwas Übung wirst du das sicher schaffen.
Here is an example:
| 3117770201 | |
| + | 1063114829 |
| + | 5737272555 |
| + | 1244685703 |
| + | 9325138635 |
| + | 8914246966 |
| + | 3734736231 |
| + | 4200292442 |
| + | 5494762027 |
| + | 1927918490 |
Then you should calculate the result. If you are right, you will come to the number 44759938079. In order to keep track, you can see the number in columns on the display.
The more you improve, the higher your level.
These are the different levels:
| Level | <=5 min | Addition | × 5 digits | Addition | × 8 digits | Addition | √ 5 min | Addition |
|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| 2 | 2 | 0 | 2 | 0 | 2 | 0 | 2 | 0 |
| 3 | 3 | 0 | 3 | 0 | 3 | 0 | 3 | 0 |
| 4 | 4 | 0 | 6 | 0 | 4 | 0 | 4 | 0 |
| 5 | 5 | 0 | 9 | 0 | 5 | 0 | 5 | 0 |
| 6 | 6 | 0 | 12 | 0 | 6 | 0 | 6 | 0 |
| 7 | 6 | 1 | 12 | 3 | 6 | 1 | 6 | 1 |
| 8 | 7 | 1 | 15 | 3 | 7 | 1 | 7 | 1 |
| 9 | 8 | 1 | 18 | 3 | 8 | 1 | 8 | 2 |
| 10 | 9 | 1 | 21 | 3 | 9 | 1 | 10 | 2 |
| 11 | 10 | 1 | 24 | 3 | 10 | 1 | 12 | 2 |
| 12 | 11 | 1 | 27 | 3 | 11 | 1 | 14 | 2 |
| 13 | 12 | 1 | 30 | 3 | 12 | 1 | 16 | 2 |
| 14 | 12 | 2 | 30 | 6 | 12 | 2 | 16 | 4 |
| 15 | 13 | 2 | 33 | 6 | 13 | 2 | 18 | 4 |
| 16 | 14 | 2 | 36 | 6 | 14 | 2 | 20 | 4 |
| 17 | 15 | 2 | 39 | 6 | 15 | 2 | 22 | 4 |
| 18 | 16 | 2 | 42 | 6 | 16 | 2 | 24 | 4 |
| 19 | 17 | 2 | 45 | 6 | 17 | 2 | 26 | 4 |
| 20 | 20 | 0 | 54 | 0 | 20 | 0 | 32 | 0 |
 Menü
Menü
